Functional Correspondence from Discrete Geometry to Learning

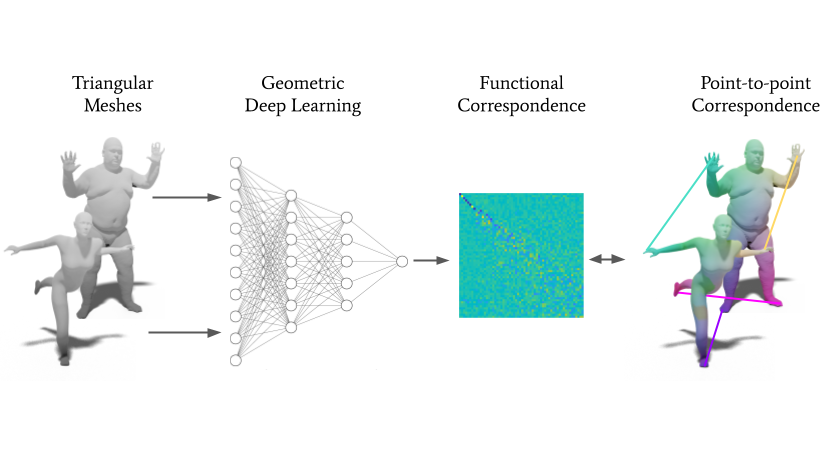
• Riccardo Marin, University of Tuebingen
• Emanuele Rodola, GLADIA

July 1st, 9:00 - 10:30

Geometry processing is a vital component for solving 3D shape-matching problems that have significant relevance in enabling various downstream tasks like artistic designs, CAD modeling, and medical analysis. With the advent of data-driven solutions, flexible alignment techniques have become essential tools to unleash the potential of deep learning methods. This tutorial introduces the Functional Maps paradigm, one of the main frameworks for the past decade. We will explain the main concepts of this elegant and flexible framework on graphs, and then develop the necessary tools for triangular mesh cases. We will review the crucial steps of this long-standing literature, from its inception to the advent of geometric deep learning. Additionally, we will highlight the latest and most promising research directions, giving participants a comprehensive understanding of the current state-of-the-art in this field.

Hands-On Introduction to FEM in Python

• Teseo Schneider, University of Victoria

July 1st, 10:45 - 12:15

The numerical solution of partial differential equations (PDEs) is ubiquitous in computer graphics and engineering applications, ranging from the computation of UV maps and skinning weights to the simulation of elastic deformations, fluids, and light scattering. The finite element method (FEM) is the most commonly used discretization of PDEs due to its generality and rich selection of off-the-shelf commercial implementations. In this course, we will implement a FE solver in 1D for the Laplace equation from scratch using only Numpy. We will briefly derive the necessary theory and quickly move into live coding the solver. At the end of the course, you will have a basic applied understanding of how the FEM works and how to extend the current code to higher dimensions and more complicated physics.

Computational Design of Deployable Structures

• Julian Panetta, UCDavis

July 1st, 13:15 - 14:45

Structures that transform from compact configurations (which are simpler to manufacture and transport) to 3D shapes with specific forms and functions have important advantages for applications like emergency shelters, temporary event spaces, medical devices, and satellite antennas. However, designing such structures is difficult, involving interesting technical challenges like controlling the highly nonlinear large-deformation behavior of elastic beam and membrane structures. This course presents computational techniques for tackling inverse design problems in this space. It will cover shape optimization using differentiable physics simulation and show various strategies for accelerating these optimization algorithms. It will also introduce two-scale design algorithms, where the low-level details of the physical system are abstracted using homogenization to obtain a coarsened design problem that can be solved robustly by traditional computer graphics techniques like surface parametrization algorithms. Then the coarsened solution is “de-homogenized” to a full-scale structure and fine-tuned with shape optimization.

A quick journey into geometry processing

• Bruno Levy, Inria

July 1st, 15:00 - 16:30

This course is a gentle introduction to the set of notions useful in geometry processing that I consider as the “minimal toolbox”. I will illustrate the different notions with tips and tricks on how to efficiently implement them in a computer. Code and demos related to the notions that I’ll present is available in Geogram (https://github.com/BrunoLevy/geogram) and Graphite (https://github.com/BrunoLevy/GraphiteThree)

Connecting Language to 3D

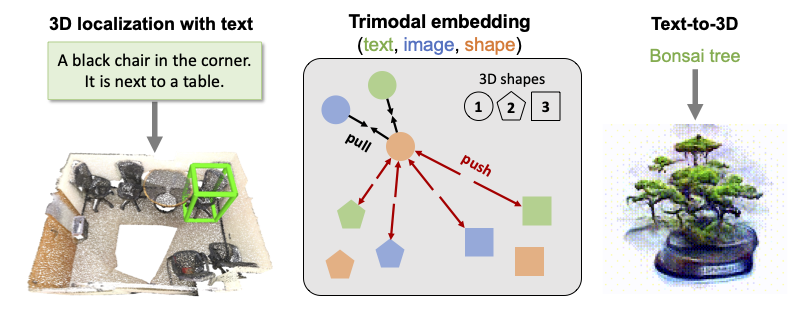
• Angel Chang, Simon Fraser University

July 1st, 16:45 - 18:15

In this tutorial, we will cover recent developments in connecting language to 3D. We will discuss components in multimodal models for language and 3D data. Then we will cover applications such as localizing and describing objects in 3D scenes, and text-to-3D shape and scene generation. We will conclude with open research challenges and opportunities in this emerging research direction.

Hexmesh generation and processing

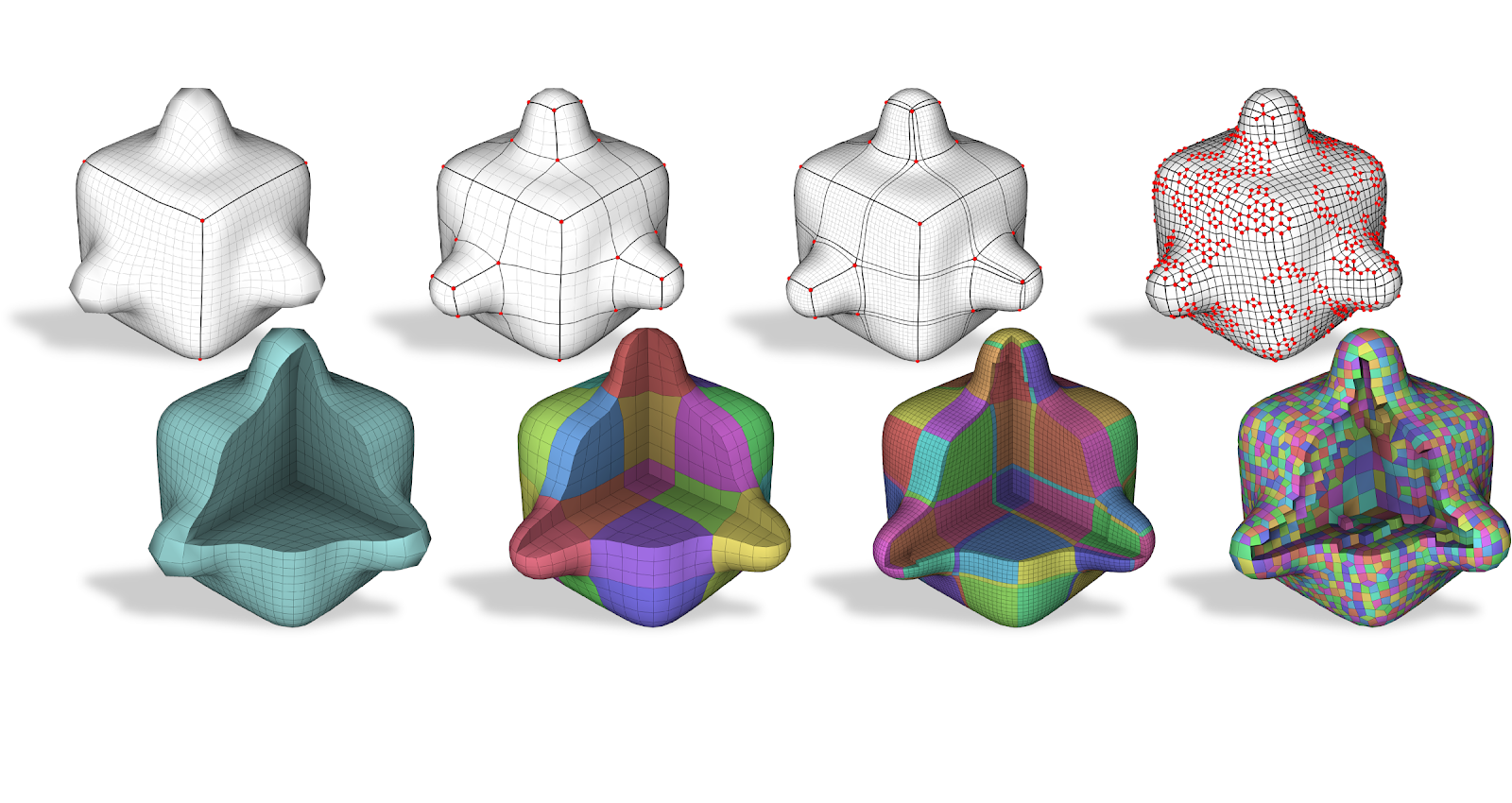
• Gianmarco Cherchi, University of Cagliari
• Marco Livesu, IMATI

July 2nd, 9:00 - 10:30

Hexahedral meshes are a prominent volumetric mesh representation. They are largely used as computational domains for the resolution of partial differential equations for physically based simulation, making them a core ingredient of many software tools used by the automobile, naval, aerospace, medical, and geological industries, as well as for many applications in Computer Graphics and Animation. In academic research and industry, the algorithmic generation and processing of hexahedral meshes have been studied for more than 30 years now. In this course, we will introduce the topic of hexahedral meshes and focus on the most relevant techniques for hexahedral mesh generation in Computer Graphics. For each technique, we will highlight capabilities and limitations, also pointing out the associated unsolved challenges. The required background, pertaining to geometrical as well as combinatorial aspects, will be introduced along the way.

Dive into Neural Implicit-Explicit 3D Representations and their Applications

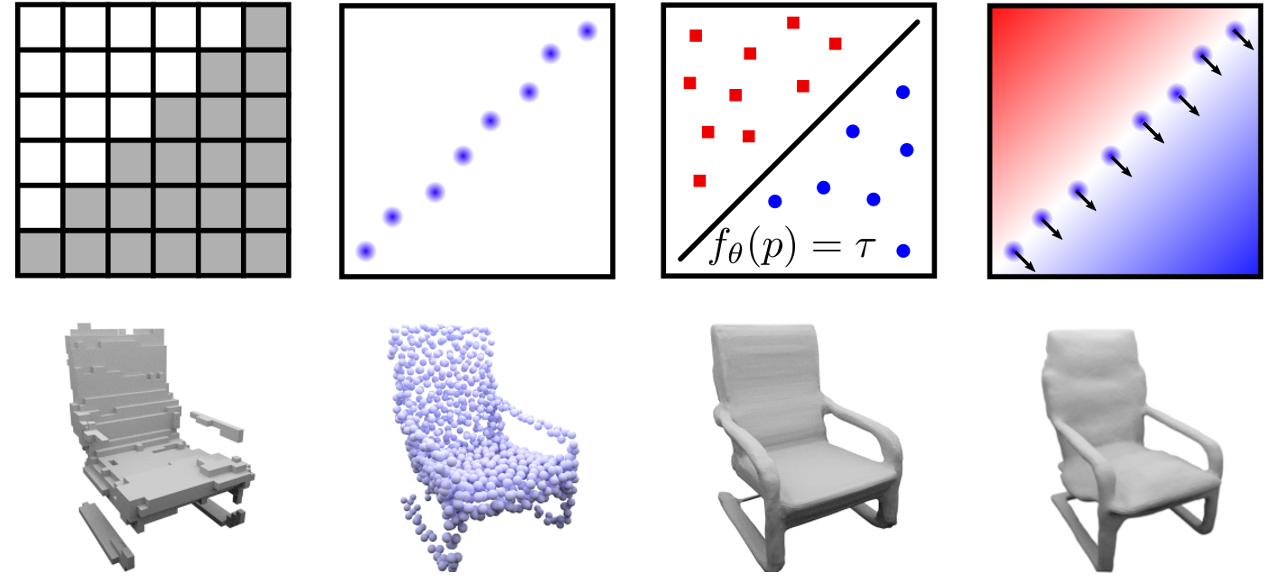
• Songyou Peng, ETH Zurich & MPI

July 2nd, 10:45 - 12:15

In this lecture talk, we will delve into the fascinating world of neural implicit-explicit 3D representations from a computer vision perspective. Beginning with the basics of explicit, implicit, and hybrid 3D scene representations, we will establish a foundation for understanding how these representations contribute to the field of 3D computer vision. We will then explore the recent evolution of hybrid implicit-explicit 3D representations in 3D reconstruction, neural rendering, and visual SLAM, discussing seminal works that have significantly advanced the state-of-the-art. In light of the recent hype surrounding ChatGPT, we will also briefly examine how large language models can be combined with implicit and explicit representations to enable new possibilities and innovative solutions in computer vision research

Topology-Aware Reconstruction

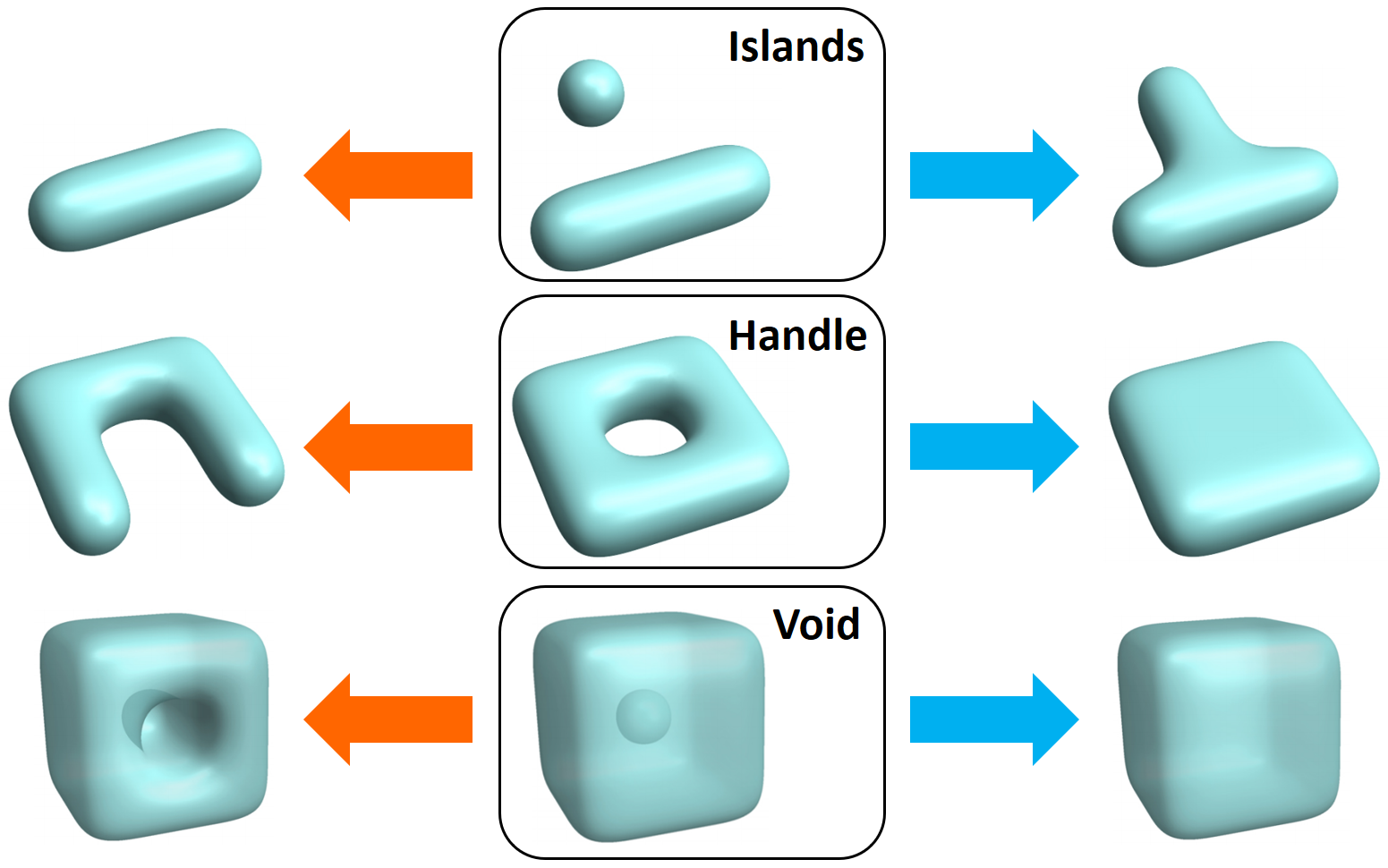
• Tao Ju, Washington University in St. Louis

July 2nd, 13:15 - 14:45

Surface reconstruction from raw and imperfect inputs often results in shapes containing unwanted topological features, such as islands, handles, and voids. These errors are detrimental to downstream geometric processing tasks such as simplification, parameterization, and simulation. Topological errors can either be removed after the shape has been reconstructed (known as topological repair) or prevented during reconstruction by imposing topological constraints. This course will introduce fundamental concepts of topology that are relevant to surface reconstruction, review existing methods for topology repair and topology-constrained reconstruction, and describe several selected methods in detail. The course will end with a discussion of open problems in this area that await future research.

Geometry Processing with Implicit Surfaces

• David R. Palmer, MIT

July 2nd, 15:00-16:30

The recent popularity of neural implicit surfaces has renewed interest in implicit representations of geometry. In this session, we will dive into the world of implicit surfaces, both classical and neural. First, we will look at the use of implicit surfaces in surface reconstruction from point clouds. We will explore how a classical method, Poisson surface reconstruction, has recently been reinterpreted in a Gaussian process framework. Then we will take a look at recent neural implicit methods for surface reconstruction and the architecture and regularization choices they make. We will take a brief detour to look at NeRF and its descendants and their relationship to neural implicit models. The success of neural implicit representations has driven an interest in building a complete geometry processing pipeline around these representations. We will look at some attempts in this direction and conclude with some reflections about the future of the field.

Machine Learning for Structural Biology

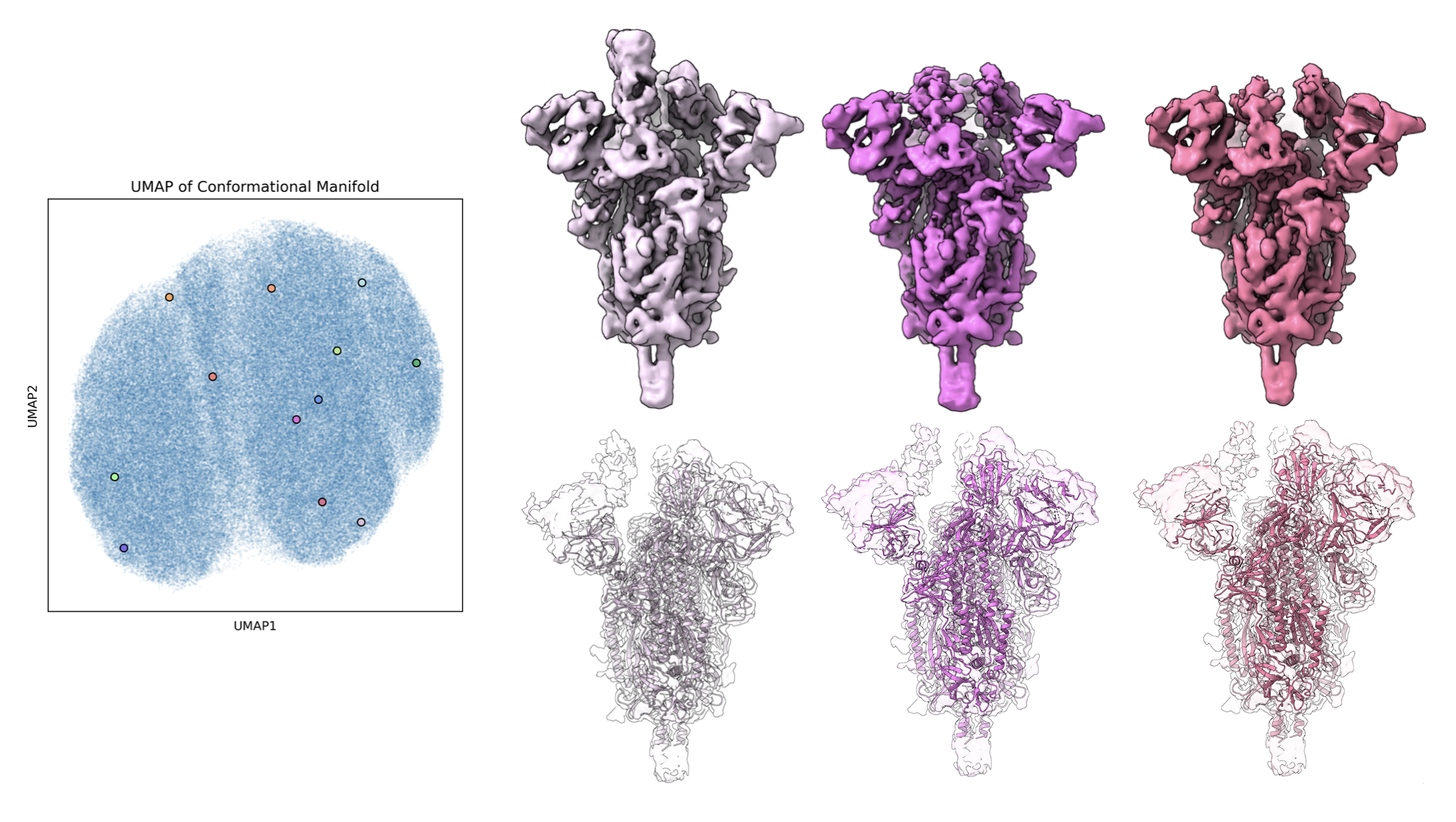
• Ellen Zhong, Princeton University

July 2nd, 16:45-18:15

Over the past few years, structural biology, the study of the 3D structure or shape of proteins and other biomolecules, has been transformed by breakthroughs from machine learning algorithms. The goal of this course will be to highlight some of these recent advances and to make connections between their underlying algorithms to related methods in geometry processing. After a brief primer on proteins and the significance of their 3D structures (assuming no prior knowledge of biology), I will overview two complementary research thrusts:

1. • protein structure prediction (e.g. AlphaFold) and
2. • protein structure determination via 3D reconstruction of cryo-electron microscopy images.

Topics will include structured transformers for 3D data and implicit neural representations, respectively. A desired outcome will be to convey the unique, multimodal challenges in this highly interdisciplinary area.